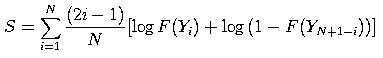K-S Test (Chakravart, Laha, and Roy, 1967) digunakan untuk menentukan distribusi suatu data sampel. Selain itu, dapat juga digunakan untuk menguji kenormalan suatu data digunakan dengan cara menstrandarkan sampel kemudian membandingkannya dengan distribusi normal. K-S Test dibentuk berdasarkan fungsi distribusi empiric (empirical distribution function – ECDF). Misal terdapat data Y1, Y2, … YN, maka ECDF didefinisikan dengan EN = n(i) / N, di mana n(i) merupakan jumlah dari Yi yang diurutkan dari kecil ke besar.
Keuntungan K-S Test adalah statistic-nya tidak bergantung pada fungsi distribusi kumulatif dari sebaran yang akan diuji. Selain itu keuntungan lainnya terletak pada exact test, yaitu chi square goodness of fit, bergantung pada suatu ukuran contoh saja. Namun K-S Test juga memiliki kelemahan, yaitu:
1. Hanya dapat diaplikasikan untuk distribusi kontinyu
2. Cenderung sensitive pada pusat distribusi
Keterbatasan untuk masalah no 2 dapat diatasi dengan menggunakan Anderson Darling test.
K-S Test Analysis
-. Hipotesis dari K-S Test:
H0: Data mengikuti sebaran normal
H1: Data tidak mengikuti sebaran nomal
-. Statistik uji:

di mana:
F merupakan fungsi komulatif distribusi yang akan diuji dan harus berupa distribusi kontinyu.
-. Significance level: alpha
-. Daerah kritis: Tolak H0 apabila nilai kritis D lebih besar dari nilai kritis pada table, atau peliang nilai kritis D lebih kecil dari significance level (alpha).
Contoh: Data tinggi badan siswa dalam cm
148.7 149.8 147.9 152.1 152.1
147.9 150.4 160.0 150.5 150.4
147.3 142.6 153.4 149.3 153.8
144.7 154.9 152.7 150.5 151.0
149.2 154.0 152.7 147.2 145.8
149.9 151.2 148.0 148.0 153.0
146.3 149.2 149.3 153.0 150.7
152.2 148.7 148.7 146.8 148.9
155.1 151.5 148.9 152.3 156.2
153.3 151.6 154.1 150.3 142.4
Sama seperti Anderson Darling Test, K-S Test juga dapat dilakukan dengan mudah melalui Minitab versi 15. Dalam software tersebut, perhitungan K-S Test dapat melalui menu Stat > Basic statistics > Normality test.

Kemudian pilih Kolmogorov Smirnov dalam menu Test of Normality.

-. Hipotesis dari Kolmogorov Smirnov Test:
H0: Data mengikuti sebaran normal
H1: Data tidak mengikuti sebaran normal
-. α : 5 %
-. Teori pengambilan keputusan:
Terima H0 -> P-Value > α.
Tolak H0 -> P-Value < α. Output Kolmogorov Smirnov Test

Intepretasi Output Kolmogorov Smirnov Test
-. Graphic: dari probability plot terlihat plot data sampel berada di sekitar garis lurus (expected value), ini menunjukkan bahwa data tinggi badan menyebar normal.
-. Statistic value
a. Mean = 150.4, rata-rata data 150.4 cm, artinya nilai memusat pada nilai 150.4 cm
b. St. Dev = 3.306, standard deviasi sebesar 3.306. Nilai standard deviasi tidak terlalu besar, ini menunjukkan keragaman data tidak terlalu besar yang artinya data bersifat homogen.
c. N = 50, jumlah sampel yang dihitung adalah 50 data d. KS = 0.057, nilai Kolmogorov Smirnov sebesar 0.057. Nilai ini relative kecil, yang berarti terima H0 atau data menyebar normal, namun dari nilai KS ini belum dapat diputuskan secara pasti apakah data menyebar normal atau tidak, karena tidak ada parameter yang pasti untuk menentukan menyebar normal.
d. P-Value = >0.150, nilai P-Value sebesar lebih dari 0.150. P-Value > 5%, artinya terima H0 yang menyatakan bahwa data menyebar normal.
Selain Minitab versi 15, K-S Test dapat juga melalui SPSS versi 16, ada dua cara untuk mendapatkan statistic dari K-S Test, yaitu melalui descriptive statistics dan nonparametric test.
1. Melalui descriptive statistics, prosedurnya adalah: Analyze > Descriptive statistics > Explore

Kemudian Explore > Plot > (klik) Normality plots with test > Continue > OK

Output K-S Test

Intepretasi K-S Test
Dari kolom kolmogorof Smirnov, nampak bahwa statistic-nya sebesar 0.067 dengan df sebesar 50, df ini adalah degree of freedom (derajat bebas) untuk kasus ini df = n, dan sig 0.200. Untuk menentukan data tersebut menyebar mengikuti sebaran normal atau tidak adalah dengan melihat sig. Sig sama seperti p-value, sehingga apabila sig > 0.05 maka terima H0, yang artinya data menyebar mengikuti sebaran normal.
2. Melalui Nonparametric test, prosedurnya adalah Analyze > Nonparametric Test > 1 Sample K-S


Output K-S Test

Intepretasi K-S Test
a. N = 50, artinya jumlah sampel sebanyak 50.
b. Mean = 150.37, artinya rata-rata sebesar 150.37
c. Standard deviation = 3.31, artinya standard deviasi sebesar 3.31, dari statistic ini terlihat bahwa standard deviasi relative kecil.
d. Positive = 0.117, artinya pengurangan antara distribusi kumulatif teoretik dengan distribusi kumulatif teoretik yang menghasilkan angka positive terbesar.
e. Negative = -0.164, artinya pengurangan antara distribusi kumulatif teoretik dengan distribusi kumulatif teoretik yang menghasilkan angka negative terbesar.
f. Absolute = 0.067, artinya dari perbandingan negative dan positif, yang terbesarlah yang dimasukkan dalam absolute.
g. Kolmogorov Smirnov Z = 0.567, artinya jika Z di bawah 1.97 maka dapat dikatakan tidak ada perbedaan antara distribusi teoretik dan distribusi empiric, dan berarti data menyebar normal.
h. Asymp. Sig. (2-tailed) = 0.905, artinya nilai ini sama seperti p-value, jika lebih besar dari 0.05 atau 5% maka terima H0 dan berarti data menyebar sesuai dengan distribusi normal.
i. Test distribution is Normal, artinya dalam table tersebut dijelaskan bahwa yang diuji adalah sebaran normal.