Mengapa data harus mengikuti sebaran normal ?
Perlu diketahui bahwa analisis yang memerlukan adanya pendugaan terhadap parameter populasi yang diamati disebut analisis parametric. Dalam pendugaan parameter umumnya menggunakan statistic uji F, t, z dan khi-kuadrat. Statistic uji tersebut (F, t, z dan khi-kuadrat) diturunkan dari sebaran normal, sehingga sebelum melakukan analisis uji parametric diperlukan asumsi kenormalan data, karena analisis ini menghendaki data yang menyebar normal. Tidak terpenuhi asumsi ini akan berpengaruh terhadap resiko salah dalam penarikan kesimpulan, sehingga akan menghasilkan kesimpulan yang kurang dapat dipercaya atau menyimpang dari keadaan yang sebenarnya, (Solimun, 1998).
Beberapa uji kenormalan antara lain:
1. Anderson Darling Test
2. Kolmogorov Smirnov Test
3. Ryan Joiner Test
4. Saphiro Wilk Test
Sebelum menjelaskan uji-uji tersebut, Anda dapat menguji kenormalan data dengan plot kenormalan data (normal probability plot), di mana plot dari data tersebut dibentuk antara nilai data dengan nilai harapan data tersebut (expected value). Nilai harapan merupakan nilai yang Anda harapkan mendekati nilai populasi sebenarnya. Jika distribusi tersebut menyebar normal, maka plot data sample berada di sekitar garis lurus, yang merupakan nilai harapan.
Probability plot dari data yang menyebar normal

Probability plot dari data yang tidak menyebar normal

Anderson Darling Test
Anderson Darling Test adalah nama dari Theodore Wilbur Anderson, Jr. (1918–?) dan Donald A. Darling (1915–?), mereka menemukan statistic untuk menguji kenormalan data, dengan jumlah data yang kecil yaitu n kurang dari sama dengan 25 (n=<25). style="font-weight: bold;">D’Angostris & Stephens (1981), menyatakan bahwa uji ini berdasarkan pada pengujian fungsi sebaran komulatif empiris yang mendasari fungsi sebaran dari data contoh. Dalam pengujian ini, fungsi sebaran empiris menaksir fungsi sesungguhnya dari sebaran tersebut, karena fungsi sebaran empiris mendekati (konvergen ke fungsi sebaran sesungguhnya). Uji ini digunakan untuk memutuskan apakah contoh acak (data) berasal dari fungsi normal atau tidak. Menurut Stephens (1974), uji Anderson Darling digunakan sebagai uji kenormalan atau kebaikan suai (goodness of fit) untuk peubah kuantitatif. Anderson Darling Test bisa digunakan untuk menguji kenormalan berbagai macam sebaran data, yaitu sebaran normal, lognormal, exponensial, weibull, sebaran logistic.
Anderson Darling Test ini digunakan untuk mengetahui distribusi dari data sampel. Uji ini merupakan modifikasi dari Kolmogorov Smirnov Test (K-S Test), yaitu K-S Test yang telah diboboti. K-S Test merupakan uji yang bebas distribusi, artinya tidak bergantung pada distribusi data tertentu yang diuji. Sedangkan Anderson Darling Test, menggunakan distribusi data tertentu dalam menghitung nilai kritis. Kelebihan Anderson Darling Test adalah uji ini lebih sensitif daripada K-S Test, namun mempunyai kelemahan yaitu nilai kritis tersebut harus dihitung dari setiap distribusi data sampel. Anderson Darling Test yang merupakan variasi dari Kolmogorov Smirnov Test, menggunakan p-value untuk mengukur apakah sebaran tertentu tersebut menyebar normal atau tidak. P-Value adalah peluang bahwa sampel yang diuji terletak pada distribusi normal dari suatu populasi. Jika p-value lebih kecil dari 0.05 maka tolak hipotesa awal (H0).
Dalam software Minitab versi 15, Anderson Darling Test digunakan untuk membandingkan fungsi komulatif distribusi dari data sampel (the empirical cumulative distribution function) dengan nilai harapan (expected value) dari data tersebut. Jika perbedaan nilai observasi data tersebut cukup besar maka uji ini menolak hipotesis nol (H0), yang berarti data tidak menyebar normal.
-. Hipotesis dari Anderson Darling Test:
H0: Data mengikuti sebaran tertentu
H1: Data tidak mengikuti sebaran tertentu
-. Statistik uji:

di mana:
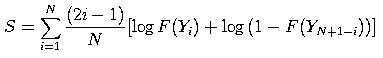
F merupakan fungsi komulatif distribusi (cumulative distribution function) dari distribusi tertentu.
-. Significance level: alpha
-. Daerah kritis: Nilai kritis dari Anderson Darling Test bergantung pada distribusi yang akan diuji. Secara statistics, keputusan menolak H0 apabila A lebih besar dari nilai kritis yang telah ditentukan.
Anderson Darling Test dapat dilakukan dengan mudah melalui beberapa software statistics, salah satunya Minitab versi 15. Dalam software tersebut, perhitungan uji Anderson Darling dapat melalui menu Stat > Basic statistics > Normality test ,

Kemudian pilih Anderson-Darling dalam menu Test of Normality.

Contoh: Data tinggi badan siswa dalam cm:
148.7 149.8 147.9 152.1 152.1
147.9 150.4 160.0 150.5 150.4
147.3 142.6 153.4 149.3 153.8
144.7 154.9 152.7 150.5 151.0
149.2 154.0 152.7 147.2 145.8
149.9 151.2 148.0 148.0 153.0
146.3 149.2 149.3 153.0 150.7
152.2 148.7 148.7 146.8 148.9
155.1 151.5 148.9 152.3 156.2
153.3 151.6 154.1 150.3 142.4
-. Hipotesis dari Anderson Darling Test:
H0: Data mengikuti sebaran normal
H1: Data tidak mengikuti sebaran normal
-. α : 5 %
-. Teori pengambilan keputusan:
Terima H0 --> P-Value > α.
Tolak H0 --> P-Value < α.
Output Anderson Darling Test

Intepretasi Output Anderson Darling Test
-. Graphic: dari probability plot terlihat plot data sampel berada di sekitar garis lurus (expected value), ini menunjukkan bahwa data tinggi badan menyebar normal.
-. Statistic value:
a. Mean = 150.4, rata-rata data 150.4 cm, artinya nilai memusat pada nilai 150.4 cm
b. St. Dev = 3.306, standard deviasi sebesar 3.306. Nilai standard deviasi tidak terlalu besar, ini menunjukkan keragaman data tidak terlalu besar yang artinya data bersifat homogen.
c. N = 50, jumlah sampel yang dihitung adalah 50 data
d. AD = 0.239, nilai Anderson Darling sebesar 0.239. Nilai ini relative kecil, yang berarti terima H0 atau data menyebar normal, namun dari nilai AD ini belum dapat diputuskan secara pasti apakah data menyebar normal atau tidak, karena tidak ada parameter yang pasti untuk menentukan menyebar normal.
e. P-Value = 0.769, nilai P-Value sebesar 0.769. P-Value > 5%, artinya terima H0 yang menyatakan bahwa data menyebar normal.

No comments:
Post a Comment