A stratified random sample is obtained by separating the population elements into group, strata, such that each elements belongs to one and only one stratum, and then independently selecting a simple random sample from each stratum. A stratified sample is obtained by independently selecting a separate simple random sample from each population stratum. A population can be divided into different groups may be based on some characteristic or variable like income of education. Like any body with ten years of education will be in group A, between 10 and 20 group B and between 20 and 30 group C. These groups are referred to as strata. You can then randomly select from each stratum a given number of units which may be based on proportion like if group A has 100 persons while group B has 50, and C has 30 you may decide you will take 10% of each. So you end up with 10 from group A, 5 from group B and 3 from group C.
The principal reasons for using stratified random sampling rather than simple random sampling are as follows:
First, the variance of the estimator of the population mean is usually reduced because the variance of observations within each stratum is usually smaller than the overall population variance.
Second, the cost of collecting an analyzing the data is often reduced by separation of large population into smaller data.
Third, separate estimates can be obtained for individual strata without selecting another sample and hence without additional cost.
Fourth, same reason with first reason, stratification may produce a smaller bound on the error of estimation than would be produced by a simple random sample of the same size. This result is particularly true if measurements within strata are homogenous.
How to draw a stratified random sample
To specify the strata, divide population into sample unit of population and placed it into its appropriate stratum. After the sampling units are divided into strata, we select a simple random sample from each stratum. We must be certain that the samples selected from strata are independent. That is, different random sampling schemes should be used within each stratum so that the observations chosen in one stratum do not depend upon those chose in another.
Stratified Sampling used to ensure representation of some group / characteristic of the population in the sample. Must know stratifying data for everyone on sampling frame. Draw a separate random sample for each category of the stratifying characteristic
a. Divide sampling frame by group
b. Use same sampling ratio to sample from within each category
Can also stratify by an interval/ordinal characteristic
a. Sort sampling frame by characteristic
b. Take a systematic sample from sorted sampling frame
Allocation of the sample
Objective of a sample survey design is to provide estimation with small variance at lowest possible cost. After the sample size n is chosen, there are many ways to divide n into individual stratum sample size, n1, n2,…, nL. Each division may result in a different variance for the sample mean. Hence our objective is to use an allocation that gives a specified amount of information at minimum cost.
Our objective the best allocation scheme is affected by three factors:
1. The total number of elements in each stratum
2. The variability of observation within each stratum
3. The cost of obtaining an observation from each stratum
We can make the following summary statement on stratified random sampling: In general, stratified random sampling with proportional allocation will produce an estimator with smaller variance than that produce by simple random sampling (with the same sample size) if there is considerable variability among the stratum means. If sampling costs are nearly equal from stratum to stratum, stratified random sampling will optimal allocation will yield estimators with smaller variance than will proportional allocation when there is variability among the stratum variances.
Estimated variance for stratified random sampling is bigger than simple random sampling. Simple random sampling may have been better than stratified random sampling for this problem.
Scheme of Stratified Random Sampling
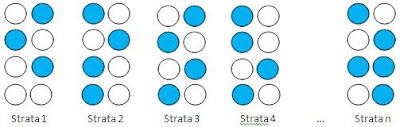
*. Blue circle show us selected sample
All strata selected became sample and every member in strata have same chance to be selected for sample
Summary
Stratified Random Sampling
• Example: The basis for forming the strata might be department, location, age, industry type, etc.
• The population is first divided into groups of elements called strata. The elements within each stratum are as much alike as possible (i.e. homogeneous group).
• A simple random sample is taken from each stratum. Formulas are available for combining the stratum sample results into one population parameter estimate.
• Advantage: Allows for a smaller total sample size
Source:
-. Richard L. Scheaffer, William Mendenhall, Lyman Ott; Elementary Survey Sampling, 4-th, PWS-Kent Publishing Company, 1990, Boston
-. Mugo Fridah W, Sampling in Research
-. SamplingBigSlides.pdf

No comments:
Post a Comment