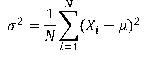Judul di atas merupakan judul salah satu jurnal statistika yang ditulis oleh Paul F. Velleman, Cornell University, dalam
Journal of Statistics Education Volume 16, Number 2 (2008), dari www.amstat.org/publications/jse/v16n2/velleman.html.
Dalam abstraknya penulis menjelaskan bahwa kekeliruan di pikiran masyarakat umum bahwa
statistics merupakan alat untuk berbohong dengan data atau
statistics merupakan alat untuk memanipulasi sesuatu dengan data. Terutama apabila dihubungkan dengan pernyataan yang berkembang dalam masyarakat yaitu
”lies, damn lies, and statistics”. Penulis menjelaskan bahwa hal ini terjadi salah satunya mungkin karena kesalahan pada proses pembelajaran, terutama pada saat menggunakan
statistics sebagai alat pengambil kesimpulan (
statistics judgement). Pengajar
statistics harus menjelaskan bahwa dalam proses
statistics judgement, murid atau mahasiswa harus bertanggung terhadap keputusan yang direkomendasikannya. Terutama pembelajaran mengenai etika-etika dalam mengambil keputusan secara
statistics melalui data yang tersedia.
Pernyataan
”lies, damn lies, and statistics” merupakan kutipan yang paling favorit dalam semua disiplin ilmu.
A Google books mencatat kata
”lies, damn lies, and statistics” terdapat dalam lebih dari 495 buku, dan
search engine google menemukan kurang lebih 207.000 lokasi yang menggunakan kata-kata tersebut. Dari sample tersebut setidaknya menunjukkan bahwa
statistics identik dengan ketidak-jujuran, manipulasi dan kebohongan.
Asal mula pernyataan
“lies, damn lies, dan statistics” berasal dari seorang penulis yang bernama Mark Twain, yang berkata
“I was deducing from the above that I have been slowing down steadily in these thirty-six years, but I perceive that my statistics have a defect: 3,000 words in the, spring of 1868, when I was working seven or eight or nine hours at a sitting, has little or no advantage over the sitting of today, covering half the time and producing half the output. Figures often beguile me, particularly when I have the arranging of them myself; in which case the remark attributed to Disraeli would often apply with justice and force: "There are three kinds of lies: lies, damn lies, and statistics." (1924 , p. 246)”.Dalam pernyataan tersebut, Twain mencoba menggunakan
statistics analysis yaitu rata-rata. Twain menghitung rata-rata ia menulis adalah 375 kata tiap jam, hitungan ini diperoleh dari 3000 kata dibagi 8 jam kerja. Artinya ia hanya menulis cukup sedikit tiap hari, bagi Twain hal ini sangat tidak masuk akal. Dari masalah ini Twain berpendapat bahwa
statistics mempunyai kelemahan, selain itu karena dengan
statistics mereka tidak tahu berapa lama ia bekerja dalam tiap hari, dan Twain juga mengatakan bahwa terdapat kesalahan dalam
statistics. Twain berpendapat bahwa hal tersebut merupakan kebohongan, sehingga ia pun setuju dengan pernyataan Disraeli mengenai
“lies, damn lies and statistics”.Penulis berpendapat bahwa sebenarnya asal usul kata
”lies, damn lies, and statistics” sebenarnya tidak jelas. Ada dua kesimpulan mengenai hal ini yaitu Twain tidak mengatakan hal itu dan bahwa Twain salah dalam mengutip pernyataan tersebut dari Disraeli. Asal perkataan tersebut sebenarnya terjadi pada tahun 1895 di Saratoga Springs, seorang ekonom dan politikus British, Leonard Henry Courtney (1832 – 1918) mengatakan bahwa :
“After all, facts are facts, and although we may quote one to another with a chuckle the words of the Wise Statesman, "Lies—damn lies—and statistics," still there are some easy figures the simplest must understand, and the astutest cannot wriggle out of.4 p. 25).”Dari pernyataan itu sangat mungkin apabila Twain salah mengutip dan mengasumsikan
“Wise Statesman” adalah Disraeli. Padahal Leonard Henry Courtney pada saat itu menjelaskan permasalahan
statistics dengan cara menghibur melalui kutipan “
Wise Statesman “. Menurut Leonard Henry Courtney,
“Wise Statesman“ sebenarnya adalah Arthur Yakobus Balfour, orang yang berpengaruh dari partai conservative selama 50 tahun dan bukan Disraeli. Arthur Yakobus Balfour dalam pidato politiknya menyindir lawan politiknya yang menggunakan
statistics untuk dalam memalsukan data.
Selanjutnya penulis menerangkan mengani makna
“truth”, menurutnya seseorang yang menggunakan
statistics untuk kebohongan dan orang yang memahami kutipan
(lies, damn lies, and statistics) sebenarnya tidak yakin bahwa tujuan
statistics adalah menyesatkan dan ketidak-jujuran. Mengenai
“truth” atau kebenaran ini penulis menjabarkan beberapa axiomanya, salah satunya adalah tujuan dari
statistics yaitu memfasilitasi penemuan, pemahaman, perhitungan, penemuan model, dan komunikasi fakta mengenai dunia. Berdasarkan axioma ini, berarti tidak mungkin
statistics diposisikan sejajar dengan
“lies and damn lies”. Dalam penerapan di kehidupan umum,
statistics seperti sebagai
”gatekeeper”.
Statistics secara
significance dibutuhkan dalam ilmu sosial, sebagai contoh dalam ilmu kesehatan,
statistics sebagai ”alat bukti”, yang untuk memilih
treatment yang tepat secara ilmiah.
Penulis juga menjelaskan mengenai fakta dan proses
statistics,
statistics memiliki dua arti yaitu
statistics berarti data yang dikumpulkan dan
statistics berarti proses dan analysis terhadap fakta-fakta untuk mendapatkan arti yang lebih dari data kemudian dari data dapat didefinisikan dan dibuat kesimpulan dan keputusan.
Seakan tidak mau kalah dengan kutipan
“damn lies”, penulis menerangkan bahwa
statistics merupakan
“damn truth”. John Tukey mengatakan bahwa
statistics lebih
“science” daripada
mathematics.
Mathematics secara theory dan dalil dapat dikatakan lebih benar, sedangkan untuk
statistics harus perlu ilmu yang menyertai agar analisanya dikatakan benar. Misal suatu data
statistics, tidak peduli bagaimana benarnya data tersebut, namun apabila cara memperolehnya tidak secara
statitics, maka data tersebut tidak dapat digunakan lagi.
Statistics lebih membahas masalah empirik daripada masalah teoritis.
Statistician bekerja dengan data dan membentuk model dari data tersebut. Pada saat model dan data menyimpang, hal itu merupakan suatu kemajuan dan bukannya suatu kegagalan. Isaac Asimov mengatakan bahwa
“The most exciting phrase to hear in science, the one that heralds new discoveries, is not 'Eureka!' but 'That's funny... ‘” Darimana anggapan
“damn lies” itu muncul ?
Statistician secara jelas mempertimbangkan kejujuran dan mengakui ketidakpastian mereka. Namun ketika
statistician melakukan kesalahan, hal ini dianggap
statistician melakukan penipuan yang disengaja dan
statistician dianggap gagal. Menurut penulis,
”lies” ini terjadi dari ketidakpastian yang terdapat dalam
statistics. Ketidakpastian dalam
statistics sebenarnya ”telah dibayar” dengan adanya interval dalam menduga nilai parameter. Tidak cukup dengan itu,
statistics juga memberikan nilai pasti dari ketidakpastian interval tersebut. Secara ilmu,
statistics bukanlah masalah algoritma atau
deterministic (kepastian), masalah dalam
statistics terjadi karena
sample yang mungkin memberikan jawaban yang berbeda, dan bukan statistician yang bekerja pada
sample yang sama memberikan jawaban berbeda.
Kemudian penulis juga menjelaskan mengenai
”statistician judgement”.
Statistical analysis atau pengambilan keputusan berdasarkan
statistics bukanlah hal yang baru dan termasuk di dalam area pengujian hipotesis. Namun banyak orang yang langsung menginginkan p-value kurang dari 0.05 tanpa mendasarkan pada pertimbangan keilmuan. Sangat mudah untuk menentukan proses hipotesis dalam
statistics atau metode ilmiah, namun perlu pertimbangan yang kuat dalam memutuskannya.
Sir Ronald Fisher, penemu
experimental design dan
analysis of variance, berpendapat bahwa
statistician terbiasa dengan p-value kurang dari 0.05 untuk diterima secara
statistics, dan inilah juga yang menjadi pedoman bagi
statistician hingga saat ini. Yang paling penting bagi pengambil keputusan yang memanfaatkan
statistical analysis adalah pengambil keputusan harus memahami masalah yang dihadapi dan pengetahuan tentang ilmu mereka.
Yang dibutuhkan judgement dalam
statistics adalah kejujuran. Untuk itu ketepatan dalam mengetahui masalah apa yang akan dibahas merupakan hal penting, terutama dalam proses
statistics judgement. Seperti dalam buku William Hunter -
"The Practice of Statistics: The Real World is an Idea Whose Time Has Come" mengatakan bahwa pertanyaan utama dari
statistician dalam menganalisa sesuatu adalah apa tujuan dari penelitian ini. Dengan mengetahui permasalahan yang akan dianalisa,
statistician dapat memperoleh petunjuk yang benar dalam menentukan
statistics judgement. Selain itu dengan mengetahui permasalahan yang sebenarnya, kejujuran dalam
statistical analysis juga dapat dipertanggungjawabkan.
Statistician dalam proses analisanya merupakan proses yang mencari kebenaran dan bukan proses yang mencari-cari kebenaran.
Jika dilihat kembali ke atas, sebenarnya Twain tidak bermaksud mencaci maki
statistics, namun lebih pada peringatan untuk masyarakat awam bahwa harus berhati-hati pada data dan output
statistics, karena bila salah dalam menafsirkan dapat mengakibatkan kesalahan yang fatal dan menyesatkan. Pendapat Twain ini setidaknya memberikan masukan pada
statistician agar dalam
statistics judgement tetap diperlukan etika sehingga tidak seolah-olah dibohongi oleh
statistics dan membohongi orang lain dengan
statistics.
(krisnafr)(diringkas sesuai dengan jurnal asli dengan keterbatasan oleh Krisna Rahmantya)