Ukuran penyebaran

Disebut juga sebagai ukuran variasi atau dispersi, ukuran ini berasal dari pemikiran bahwa ada data yang berada “di sekitar” rata-rata. Ada data yang tepat sama dengan nilai rata-rata, ada yang lebih kecil dan ada juga yang nilainya lebih besar dari rata-rata. Artinya bahwa antara tiap-tiap data dengan rata-rata terdapat jarak atau dispersi, begitu pula dispersi juga terdapat antara data yang satu dengan yang lain. Ukuran variasi antara lain simpangan baku (standard deviation), koefisien variasi (coefficient of variation), jarak (range) dan rata-rata simpangan (mean deviation). Ukuran variasi diperlukan karena ukuran ini memberikan informasi mengenai sebaran nilai pada data tersebut. Selain itu ukuran ini dapat digunakan untuk membandingkan sebaran dari dua distribusi data.

Simpangan baku (standard deviation), ukuran variasi ini paling banyak digunakan karena mempunyai sifat mathematics yang berguna untuk teori dan analisis. Simpangan baku diperoleh dari akar dari ragam (variance). Variance adalah rata-rata dan kuadrat dari selisih tiap-tiap data dengan mean-nya. Simbol untuk variance adalah σ2 atau sigma kuadrat. Simpangan baku memiliki satuan yang sama seperti satuan data aslinya, sehingga kelemahannya apabila membandingkan dua atau lebih data yang berbeda satuan maka pembandingan akan sulit dilakukan.
Variance untuk populasi rumusnya:

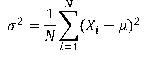
Variance untuk sampel rumusnya:
atau
Untuk simpangan baku populasi rumusnya:

Simpangan baku untuk sampel rumusnya:
atau

Terdapat perbedaan pembagi pada populasi dan sampel, pada populasi pembagi adalah n sedangkan pada sampel pembagi adalah n-1. Perbedaan ini karena pada sampel hanya mengestimasi populasi, artinya nilai sampel hanya mendekati dan bukan nilai yang menggambarkan nilai sebenarnya pada populasi. Pembagi pada sampel (n-1) disebut dengan derajat bebas (degree of freedom). Dapat ditunjukan secara statistika matematis bahwa dengan pembagi (n-1), variance sampel merupakan “unbiased estimate” bagi variance populasi.

Nilai jarak (range), merupakan ukuran variasi yang paling sederhana dan mudah untuk dihitung. Data diurutkan dahulu dari yang terkecil hingga terbesar kemudian dihitung selisih antara data terbesar dan data terkecil.
Rumusnya; Nilai jarak = X(n) – X1. Range merupakan ukuran yang kasar untuk n besar dan ukuran ini kurang sensitive, artinya bahwa informasi bisa menyesatkan apabila ada dua data yang memiliki kisaran sama tapi simpangan baku yang berbeda. Range ini tidak selalu dapat menggambarkan keragaman data untuk n besar.

Rata-rata simpangan, seperti namanya perhitungan ini dilakukan dengan cara merata-ratakan simpangan data. Simpangan data adalah selisih tiap-tiap data dengan rata-ratanya. Rata-rata simpangan adalah rata-rata hitung dari nilai absolute dari simpangan, rumusnya:


Koefisien variasi , pengukuran ini bermula dari simpangan baku atau standard deviation yang mempunyai satuan yang sama dengan satuan data aslinya, hal ini merupakan kelemahan apabila kita ingin membandingkan dua atau lebih kelompok data yang satuannya berbeda.
Agar dapat membandingkan dua atau lebih kelompok data dengan satuan yang berbeda maka digunakan Koefisien Variasi (KV), yang bebas dari satuan data asli.
Koefisien variasi untuk populasi

Koefisien variasi untuk sampel

Jika ada dua kelompok data dengan KV1 dan KV2, di mana KV1 > KV2, maka kelompok data pertama lebih bervariasi atau lebih heterogen daripada kelompok data kedua. Koefisien Variasi (KV), dapat juga digunakan untuk menentukan apakah kelompok data tersebut memiliki konsistensi atau tidak. Semakin besar KV maka semakin tidak konsisten, begitu pula sebaliknya semakin kecil KV semakin konsisten.